6. 선형회귀모델 (파라미터 구간추정, 가설검정)

비용함수를 최소화하는 파라미터 값을 찾는 것이 선형회귀모델의 중점

 

추청량이란?

 

        샘플(데이터)의 함수형태는

        X, Y로 이루어진 함수이다.

         추정량을 통해 알려지지 않은 파라미터 (B0, B1)를 추청가능하다.

 

 

 

1. 점추정

 

특정한 값(점)으로 파라미터를 추청하는 것

확률오차 가정에서 실제 Y 예측 Y의 오차가 시그마 제곱의 값이라는 부분이 있었는데 

그 시그마 제곱도 점추청 사용가능하다.

1 / 관측치 개수-2 * (관측치의 각 잔차e를 제곱해 모두 더함)

 

 

2. 최소제곱법으로 만든 추정량의 성질

 

가우스 마르코프의 증명

 

ㄱ. 불편추정량: 추정량의 기대값이 모수와 같아지는 추정량을 불편추정량이라 한다.

?

이해하기 쉽게 풀어써보자.

최적의 파라미터를 추청하기 위해 만든 함수식 

B0햇 = Y바-B1햇X바

파라미터 = 함수식 이므로

파라미터인 B0햇, B1햇도 추정량이다.

데이터 전체의 모집단에서 trainning data와 test data를 특정 비율로 추출 한다.

1번째 표본집단 trainning data로 최소제곱법을 시행하여 B0,B1을 도출 한 값,

2번째, 3번째......N번째 까지 표본집단의 B0,B1값을 도출하고 모든 B0,B1값을 더하고

추출한 표본집단의 개수로 나누면(평균을 내면) 모집단이 가진 최적의 파라미터 B0,B1과 동일한 값이 된다.

 

B0햇(예측한 절편), B1햇(예측한 기울기)의 기댓값(평균)=B0(파라미터),B1(파라미터)이 되면 불편추정량이다.

 

ㄴ. 다른 불편추정량보다 적은 분산을 가진다.

최소제곱법으로 계산한 점추정량은 다른 어떤 불편추정량보다 분산이 적다.

>> 잔차가 다른 주청방법을 사용했을 때보다 적어서 더욱 정확한 모델을 만들 수 있다는 의미일까?

 

 

3. 구간추정

구간추청이란?

특정 값이 아닌 값을 가질 수 있는 구간을 추정하는 것이다.

점추청량, 상수값, 점추정량의 표준편차 값을 알아내야 계산가능하다.

구간추정 = 점추청량을 중심으로 상수값을 곱한 표준편차를 더하고 뺀 범위이다.

 

 

4. 기울기 B1에 대한 신뢰구간(구간추청)구하기

구간추청의 요소

ㄱ. 최소제곱법으로 도출한 기울기 B1

 

ㄴ. 유의수준과 t분포 값 (정규분포보다 평평하고 두꺼운 좌우대칭의 분포)

유의수준(허용오차수준 이라고도 하며 표본집단에서 오차가 발생할 가능성을 의미)

신뢰수준(표본집단을 얼마나 믿을 만 한지, 집단내 오차가 발생하지 않을 가능성을 의미)

1-신뢰수준=유의수준(허용오차수준) a

자유도(주어진 조건하에서 통계적 제한을 받지않고 자유롭게 변화를 줄 수 있는 원소의 수)

 

예를 들어 표본집단들의 통계량의 기대값을 취하면 모집단의 통계량이 된다.

모집단의 평균이 100이라면 표본집단 i개의 평균에 기대값을 취했을 때 100이 되어야 한다.

이때 마지막 i-1번째 표본집단의 평균은 반드시

모든 표본집단의 평균의 합 / i(포본집단의 개수)=100이라는 값이 되어야 하기 때문에

자유롭게 변화하지 못하고 정해진 값이 된다.(자유도는 N-1개)

이처럼 통계적 모수를 알아내기 위한 함수식에서 자유롭게 변화하는 원소의 개수를 정의한 것이 자유도의 개념이다. 

함수안에 들어있는 정해진 값(모집단 평균, 모집단 분산, 이미 구한 파라미터 등) 값만큼 N-? 빼면 자유도가 도출된다.

 

ㄷ. 최소제곱법으로 도출한 기울기 B0의 표준편차

 

단순선형회귀모델 가설검정

가설 = 실험자가 실험에서 추측한 원리 

귀무가설(보편적으로 인정된 가살)과 대립가설(실험을 통해 귀무가설을 기각시킬 수 있는 가설)

실험자가 함수로 만들어논 X,Y의 관계에서 X가 정말 Y에 영향을 주는지(즉 B1이 0이 아님이 확실한지)

검증하는 과정

 

검정 통계량 t*(티스타)

귀무가설: B1은 0이다 =  X와 Y가 관계없음

대립가설: B1은 0이 아니다 = X와 Y가 관계있음

 

t*

점추정량 값         -    귀무가설로 정해논 0 / 스캐일링

 최소제곱법으로 구한 B1과       귀무가설로 추측한 B1(0)의 차이를 구한다.

 

P-value 

P = 분포에서 검정통계량 값을 넘어간 구간이 나올 확률 

검정통계량 (t*)값이  5= t분포에서 5보다 큰 값이 속한 부분의 확률

전체 t분포/ t분포에서 5보다 큰 값의 범위 

대부분 0.05, 0.01이 기준>> 이부분 추가공부필요

 

P-value 값이 클 경우 내가 정한 귀무가설이 실제 데이터와 괴리가 있으로므

대립가설을 채택해야 한다는 의미

0에 가까우면 귀무가설 채택

 

 

실제 프로그램을 사용한 검정과정

 

점추청으로 구한 파라미터값은 무엇인가요?

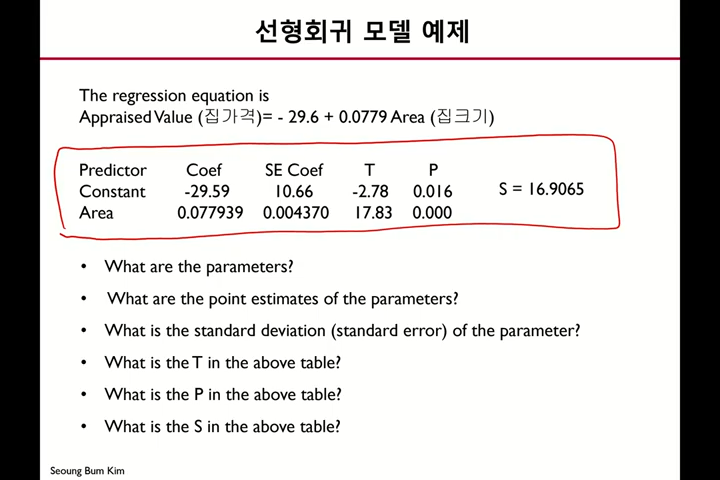
파라미터 B0,B1

점추청량 B0=-29.59 B1=0.077939

 

 

구간추정에 사용되는 표준편차값은 무엇인가요?

B0의 표준편차 10.66

B1의 표준편차 0.004370

 

 

t* 값은 얼마인가요?

점추정량-귀무가설의 0/ 스캐일링=17.83

 

 

P-value는 얼마인가요?

검정통계량 t*인 17.83이 t분포에서 나올 수 있는 확률=0.000

 

 

결론은?

우리가 설정했던 귀무가설(집크기는 집가격에 영향이 없다.)을 기각하고

대립가설(X,Y 사이에 유의미한 영향이 있다.)을 채택해야 한다는 의미이다.

 

오차향의 표준편차 S